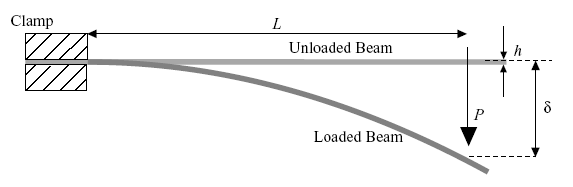
A cantilever beam is a structure that is supported on one end and protrudes into open space on the other end. It is commonly used in construction and engineering applications to support loads, such as bridges and balconies. The deflection of a cantilever beam refers to the amount of bending or displacement that occurs under a given load.
The theory of cantilever beam deflection can be understood by considering the forces acting on the beam and the material properties of the beam itself. When a load is applied to the free end of a cantilever beam, it will cause the beam to bend. The amount of bending or deflection is determined by the distribution of the load along the beam, the length and cross-sectional area of the beam, and the elastic modulus of the beam material.
The distribution of the load along the beam is important because it determines the amount of bending moment, or the rotational force, that is applied to the beam. The longer the beam, the greater the bending moment and the more deflection that will occur.
The cross-sectional area and elastic modulus of the beam material also play a role in determining the amount of deflection. A beam with a larger cross-sectional area will be able to withstand a greater load before experiencing significant deflection, while a beam with a higher elastic modulus will be more resistant to deflection under a given load.
There are several methods that can be used to calculate the deflection of a cantilever beam, including the use of beam deflection formulas and finite element analysis. These methods take into account the factors mentioned above, such as the load distribution, beam length, and material properties, to determine the amount of deflection that will occur under a given load.
In conclusion, the deflection of a cantilever beam is determined by the distribution of the load along the beam, the length and cross-sectional area of the beam, and the elastic modulus of the beam material. These factors can be taken into account using various methods, such as beam deflection formulas and finite element analysis, to calculate the amount of deflection that will occur under a given load.