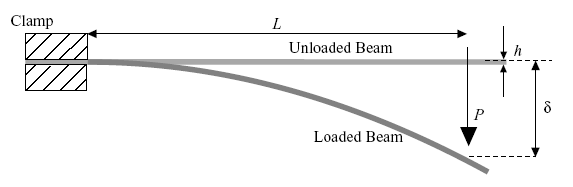
A bending of beam experiment is a common laboratory experiment in which the deformation of a beam under load is studied. The goal of this experiment is to understand how the beam behaves under different loads and how the various physical properties of the beam, such as its material properties and cross-sectional shape, affect its response to these loads.
The experiment is typically set up as follows: a beam is placed on two supports, with one end of the beam clamped to a fixed support and the other end resting on a moveable support. A load is then applied to the beam at various points along its length, and the deformation of the beam is measured using a displacement sensor or a strain gauge.
There are several factors that can affect the bending of a beam. These include the material properties of the beam, such as its Young's modulus (a measure of its stiffness) and Poisson's ratio (a measure of its lateral strain under load); the cross-sectional shape of the beam, such as its width, height, and shape; and the type and magnitude of the load applied to the beam.
In the bending of beam experiment, the results of the measurements are typically plotted as a graph showing the relationship between the applied load and the beam's deformation. This graph can be used to determine the beam's stiffness and its ability to resist bending under different loads.
One of the key findings from the bending of beam experiment is the relationship between the applied load and the beam's deformation, known as the beam's bending moment. This relationship is described by the beam's bending moment equation, which is a mathematical expression that relates the applied load, the beam's cross-sectional shape, and its material properties.
In conclusion, the bending of beam experiment is a useful tool for studying the deformation of beams under load and understanding how various factors, such as material properties and cross-sectional shape, affect the beam's response to these loads. This knowledge can be used to design stronger, more efficient beams for a variety of engineering applications.