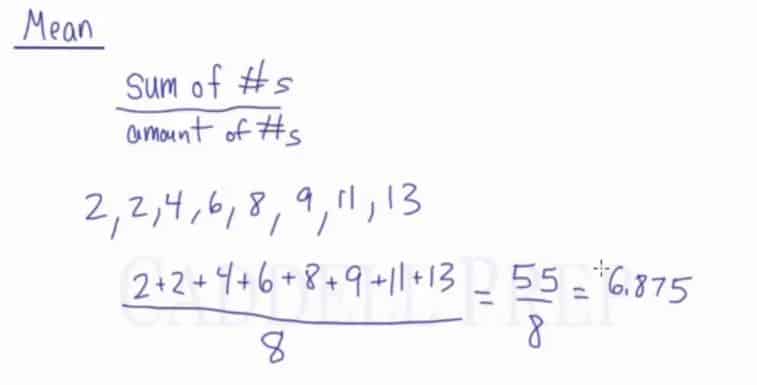Measures of central tendency, also known as statistical averages, are used to summarize and describe the characteristics of a set of data. The three most common measures of central tendency are the mean, median, and mode. Each of these measures has its own unique characteristics and is used in different situations depending on the nature of the data.
The mean, also known as the average, is calculated by adding up all the values in a dataset and dividing by the number of values. The mean is a useful measure of central tendency when the data is continuous and follows a normal distribution, meaning that the majority of the values are clustered around the center and there are fewer extreme values. However, the mean can be affected by outliers, or extreme values that are much higher or lower than the majority of the data. This can cause the mean to be misleading, as it may not accurately represent the majority of the data.
The median is the middle value in a dataset when the values are arranged in numerical order. To find the median, the data must first be sorted from smallest to largest. The median is a useful measure of central tendency when the data is skewed or has outliers, as it is not affected by extreme values. The median is also useful when the data is ordinal, meaning that it is ranked or has categories, as it does not require the data to be continuous.
The mode is the most frequently occurring value in a dataset. The mode is a useful measure of central tendency when the data is categorical, as it represents the most common category. However, a dataset may have multiple modes, or no mode at all if no value occurs more frequently than the others.
Measures of central tendency are useful for summarizing and understanding large datasets. For example, a business may use the mean to determine the average salary of its employees, or the mode to determine the most popular product among its customers. In research studies, measures of central tendency are often used to report the results of experiments, as they provide a quick and easy way to understand the main findings.
In conclusion, measures of central tendency are useful tools for summarizing and describing the characteristics of a dataset. The mean, median, and mode are the three most common measures of central tendency, and each has its own unique characteristics and uses depending on the nature of the data. These measures are widely used in various fields to understand and analyze data, and are essential for making informed decisions and conclusions.