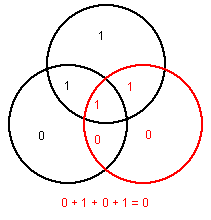Hamming code example with solution. CMSC 121: Hamming Codes 2022-10-27
Hamming code example with solution
Rating:
9,8/10
682
reviews
The role of armed forces in disaster management is a crucial one, as they are often called upon to provide assistance and support in times of crisis. Whether it is a natural disaster, such as a hurricane or earthquake, or a man-made disaster, such as a terrorist attack, the armed forces are trained and equipped to handle a wide range of situations.
One of the primary roles of the armed forces in disaster management is to provide rescue and recovery efforts. This may involve airlifting stranded individuals to safety, providing medical care to those who are injured, and clearing debris to make roads and other infrastructure passable again. The armed forces also play a key role in providing logistical support, such as setting up temporary shelters, distributing food and water, and coordinating with other agencies to ensure that aid is delivered efficiently.
In addition to rescue and recovery efforts, the armed forces may also be called upon to provide security and maintain order in the wake of a disaster. This may involve patrolling affected areas, setting up roadblocks and checkpoints, and working with local law enforcement to ensure the safety of affected communities.
Another important role of the armed forces in disaster management is to provide intelligence and communication support. This may involve gathering and analyzing information about the disaster, as well as maintaining and repairing communication systems that have been damaged or disrupted.
Finally, the armed forces may also be called upon to provide long-term support and reconstruction efforts following a disaster. This may involve rebuilding infrastructure, such as roads, bridges, and buildings, as well as providing technical assistance to local communities as they recover and rebuild.
In conclusion, the role of the armed forces in disaster management is critical, as they provide a range of essential services and support in times of crisis. Whether it is providing rescue and recovery efforts, maintaining security and order, gathering and analyzing intelligence, or providing long-term reconstruction support, the armed forces play a vital role in ensuring the safety and well-being of affected communities.
Hamming Code in Computer Networks
Dinesh has written over 500+ blogs, 30+ eBooks, and 10000+ Posts for all types of clients. Hence the bit value for P3 is 1. Now, the corrected sequence will be obtained by summing the received sequence and error sequence. About Dinesh Thakur Dinesh Thakur holds an B. I wouldn't, but that is besides the point here.
Next
Hamming Codes
And after this, no significant data bits to be considered are present thus we will stop here. If no errors occur, you will be able to decode the information bits correctly via syndrome decoding. Data Hamming code 000 110100 001 100001 010 010010 011 000111 100 001100 101 011001 110 101010 111 111111 Notice that this is the same Hamming code, except for order, as the previous example. For example, suppose we are using three bit codes, and the legal codes are 001, 010, 100, and 111. This can cause the data to be further errored.
Next
Hamming code for single error correction, double error detection

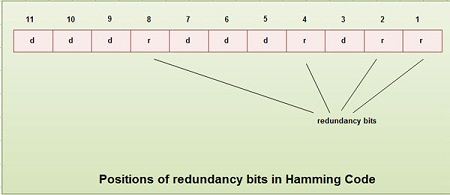
So, can someone guide me with an example on how to detect 3 bit error per code in 8,4 Hamming code? To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. The addition of the fourth row effectively computes the sum of all the codeword bits data and parity as the fourth parity bit. It covers all bit positions whose binary representation includes a 1 in the i th position except the position of r i. Here is the general method to obtain a Hamming code using parity bits. Hamming Code for double error detection The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.
Next
CMSC 121: Hamming Codes
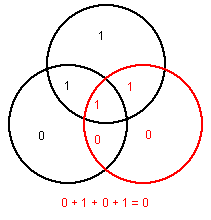
Indeed, if an invalid code is received, and we assume only one transmission error, we can correct the error by substituting the closest legal code word from the diagram. Suppose if k denotes the length of information bits and n denotes the total length of the coded bits then the length of parity or redundant bits can be obtained by getting the difference between the length of coded bit and length of information bits i. There are eight possible values, which can be represented as vertices of a cube. The r redundant bits placed at bit positions of powers of 2, i. The following formula is used to find the number of redundant bits. The resultant binary word is 0111. The usual practice aka Maximum Likelihood decoding is to assume that the number of errors is as low as possible, but it may, of course have been higher.
Next
Error Correcting Codes
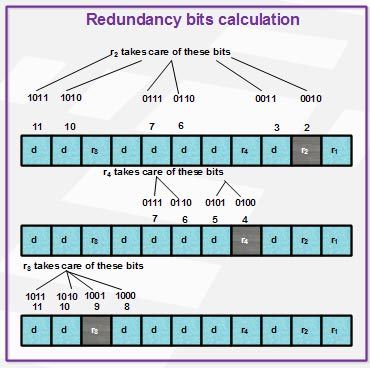
Thus, in hamming code arrangement for the obtained sequence, it will be written as: Lastly, we will go for a parity check. In other words, we want to be able to reliably transmit any of the six data strings 000, 001, 010, 100, 101, 110, and 111. Find and correct the error. There is one 1 in this group, which is wrong for even parity. On checking, the condition has been satisfied thus, we analyzed that here the total message bits are 5 and total parity bits are 4. These redundant bits are mostly inserted and generated at certain positions in the message to accomplish error detection and correction process.
Next
Hamming Code in Computer Network

Similarly, we could get the Hamming code for any of the other possible combinations of 11 data bits. Here are the results. Now there are Hamming distances of 1, 2, and 3. It is likely to be affected by external noise or other physical failures. Therefore, it must have been 000. If a code can detect, but not correct, five errors, what is the minimum Hamming distance for the code? Otherwise, a double bit error has occurred.
Next
Hamming code Implementation in Java

Suppose the following string of codes was received. In case if there is no remainder, then the data unit is assumed to be correct and is accepted. Can we correct them? There is a quick way to correct an error in a Hamming code that was derived using parity as above. Suppose that we want to be able to transmit three data bits and to be able to detect and correct single bit errors in transmission. The invalid codes 001, 010 and 100 correct to 000; while 011, 101, and 110 correct to 111.
Next
Hamming code

Hamming code can only detect 2-bit error and can correct a single bit error only. Typically, they are added at positions that are powers of 2, i. If these errors are not detected and corrected, then the data will be lost. In position 2 odd parity so set position 2 to. The various r bits are placed at the position that corresponds to the power of 2 i. Bits 3 and 6 are 00, so set bit 2 to 1 for odd parity.
Next
Hamming Code: Error Detection and Correction with Examples

If 01 or 10 are received, we know an error has occurred. Can the following pairs be legal code words? The error is detected in the data bit D4. This provides ten possible combinations, enough to represent the digits 0—9. Can we correct single transmission errors? Bits 3 and 6 are 01, so bit 2 is correct. It is a technique developed by R.
Next
How to find hamming code in C++
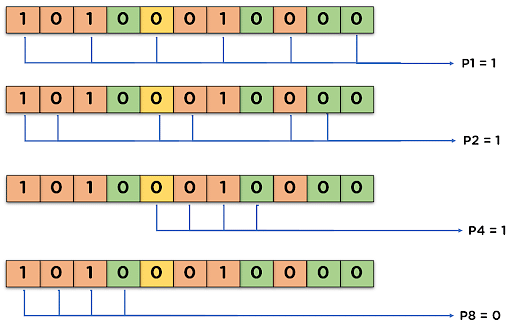
The number of redundant bits can be obtained by: : P is the number of parity bits, k is the number of information bits. } For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. In a taped interview, Hamming said, "And so I said, 'Damn it, if the machine can detect an error, why can't it locate the position of the error and correct it? If a code can detect and correct five errors, what is the minimum Hamming distance for the code? The Hamming distance between 1101 and 1011 is 2, since they differ in two positions. For instance , 000 and 111 differ in three positions. . The bit is flipped converted from 0 to 1 or vice versa to get the correct message. It could not have been 111, because that would have been two errors.
Next