Complex numbers are a mathematical concept that have found numerous applications in electrical engineering. They consist of a real part and an imaginary part, and can be represented in the form a + bi, where a is the real part and bi is the imaginary part. The imaginary unit, denoted by "i", is defined as the square root of -1.
One of the main uses of complex numbers in electrical engineering is in the analysis and design of electrical circuits. Complex numbers are particularly useful in this context because they allow engineers to represent both the magnitude and phase of a quantity, such as an electrical current or voltage.
For example, consider an electrical circuit that contains an inductor, which is a passive electrical component that stores energy in the form of a magnetic field. The current through an inductor is not in phase with the voltage across it, meaning that the phase angle between the current and voltage is not zero. By representing the current and voltage as complex numbers, it is possible to easily calculate the phase angle between them, which is important for understanding the behavior of the circuit.
Another important use of complex numbers in electrical engineering is in the analysis of alternating current (AC) systems. AC systems are commonly used to distribute electrical power over long distances, and the voltage and current in these systems oscillate at a specific frequency. By representing the voltage and current as complex numbers, it is possible to analyze the phase relationship between them, as well as the power being transmitted in the system.
Complex numbers are also used in electrical engineering to represent the impedance of electrical components, such as resistors, capacitors, and inductors. Impedance is a measure of the opposition to the flow of electrical current in a circuit, and it is complex-valued because it includes both resistance (a real quantity) and reactance (an imaginary quantity). By representing impedance as a complex number, it is possible to easily calculate the total impedance of a circuit, which is important for understanding the behavior of the circuit.
In summary, complex numbers are an essential tool in electrical engineering, with numerous applications in the analysis and design of electrical circuits, the analysis of AC systems, and the representation of impedance. Their ability to represent both magnitude and phase makes them a powerful tool for understanding and predicting the behavior of electrical systems.
Why are complex numbers important in electrical engineering
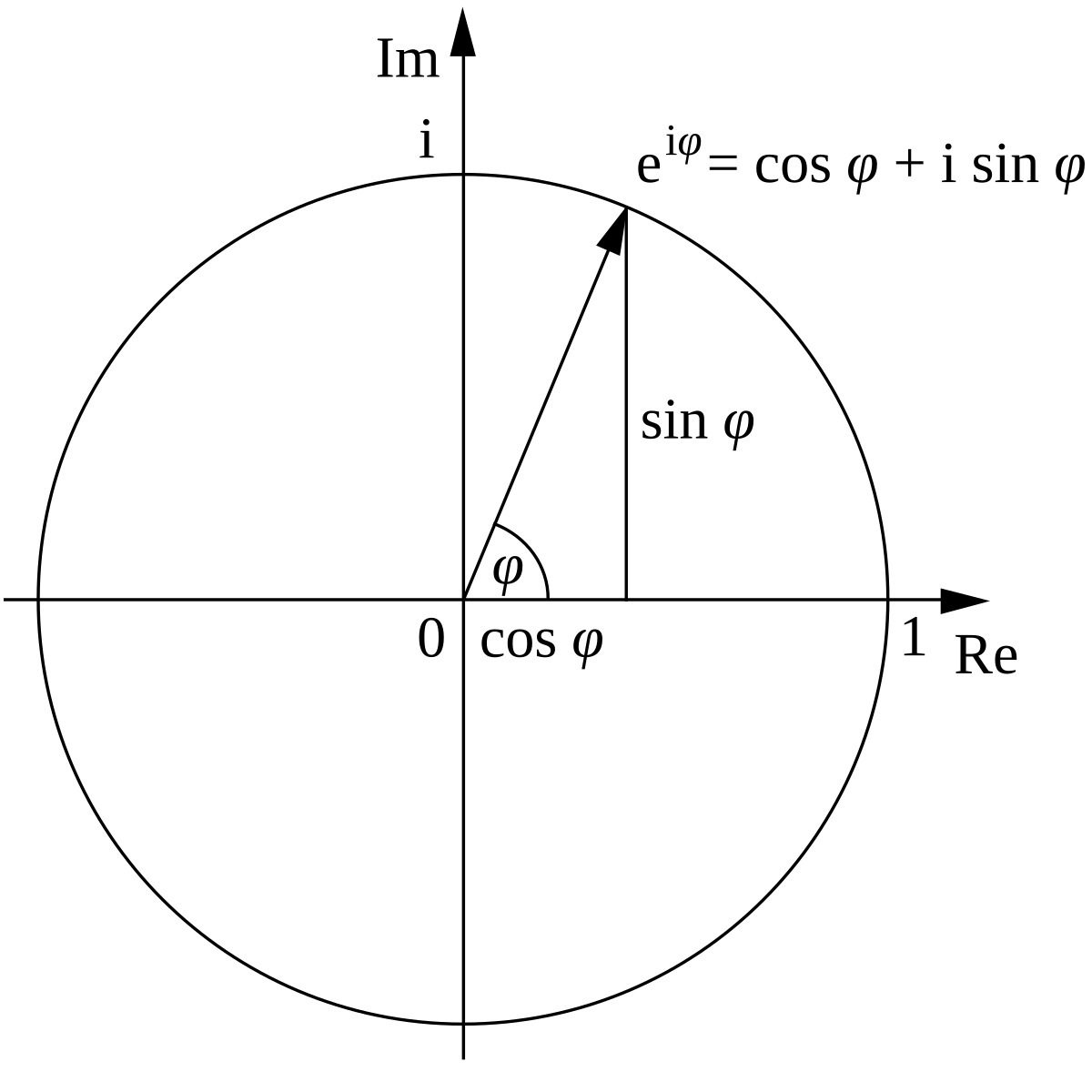
Oh, it's just the set theory version of a function. Although imaginary numbers are not commonly used in daily life, in engineering and physics they are in fact used to represent physical quantities such as impedance of RL, RC, or RLC circuit. What is the significance of complex numbers? This then produces a complex plane with four quadrants called an Argand Diagram as shown below. This approach is called phasor calculus. It is fuzzy, but somewhere along the line, mathematicians added the concept of non-integer or rational numbers, e. Complex numbers, triangles, circles, and sine waves are related.
Complex Numbers & Phasors in Polar and Rectangular Form

It's quite useful in circuit analysis - unfortunately, it's also quite limited, since it only applies to resistors. So it certainly doesn't hurt to dig a little deeper into the theory of complex numbers and complex functions. In short, they are critical to modern electrical engineering, a realization made over a century ago. It provides powerful tools for doing mathematical analysis, and often yields pleasing and unanticipated answers. Application in electronics engineering Information that expresses a single dimension, such as linear distance, is called a scalar quantity in mathematics. So now you know what impedance is. But it only applies to clean sine waves? Yes, electrical engineers use them as they are a mathematical representation of alternating current.
Application of Complex Numbers (Electrical Engineering)

You'll hear a ton of different terminology, and linear algebra is where you're really slammed with modern mathematical rigor and formalisms. When the complex number is purely imaginary, such as a real part of 0 and an imaginary part of 120, it means the voltage has a potential of 120 volts and a phase of 90°, which is physically very real. An imaginary number is a complex number with no real part, such as or. I just use complex numbers every day without thinking about it. Theroot locus,Nyquist plot, andNichols plottechniques all make use of the complex plane. This is exactly what Maxwell's equations do.
Can Someone Explain how Complex Numbers are Used in Electrical Engineering? : math
The two dimensions, length and angle, allows us to calculate amplitude and phase together, and keep them consistent. Resistors, capacitors, and inductors are characterized by their effect on the relationship between the voltage and current. Related Questions Complex numbers are used in electronics and electromagnetism. Although imaginary numbers are not commonly used in daily life, in engineering and physics they are in fact used to represent physical quantities such as impedance of RL, RC, or RLC circuit. This representation is known as the Cartesian form of z. Thanks and regards, Sara Good point.
Application of complex number in engineering
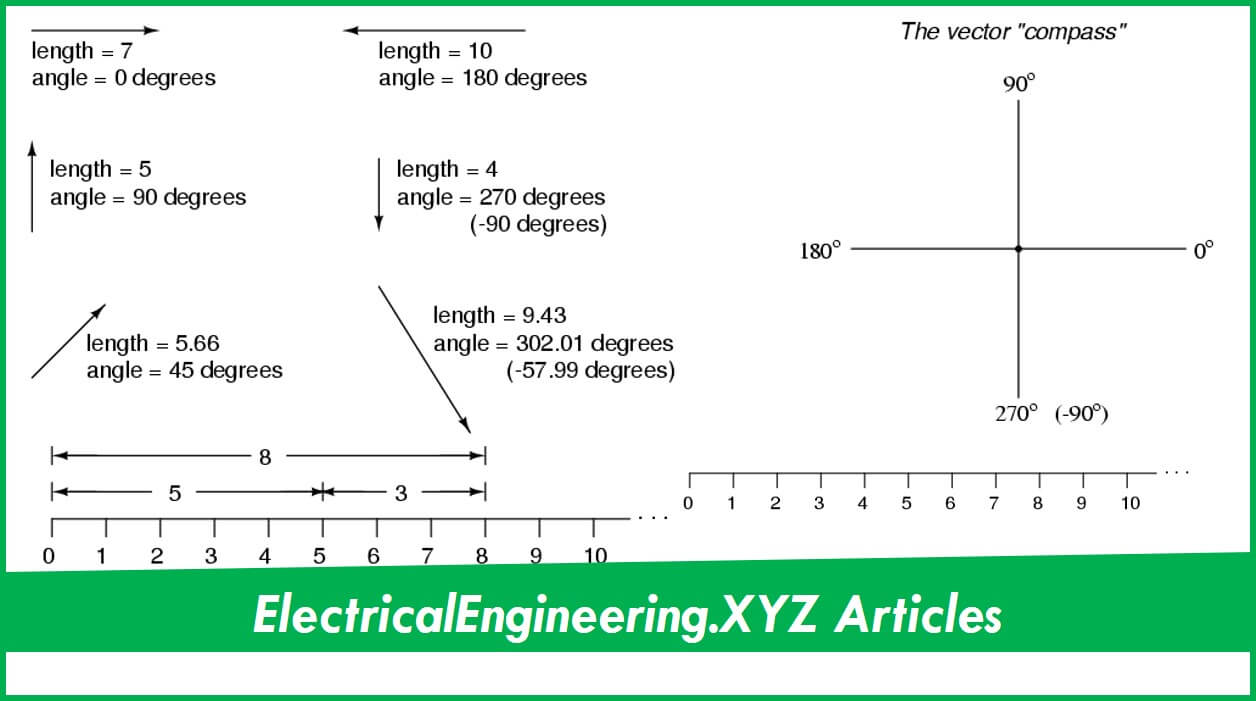
This then produces a two dimensional complex plane with four distinct quadrants labelled, QI, QII, QIII, and QIV. The math could be performed with sin and cos, but if you used Euler's formula and work in the complex plane, the math becomes 50% simpler. I have done some research concerning impedances and understand how they are written in complex form, however I am still confused why complex numbers are necessary in this field over regular numbers. The conjugate of a complex number is an important element used in Electrical Engineering to determine the apparent power of an AC circuit using rectangular form. Then angles between 0 and 90 o will be in the first quadrant I , angles θ between 90 and 180 o in the second quadrant II. This website is a very good resource and will do a good job at explaining these concepts.







