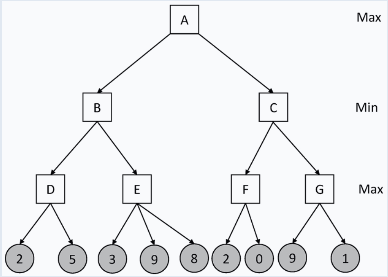
The minimax algorithm is a search algorithm used in decision-making and game theory to determine the optimal move for a player, assuming that the other player will also play optimally. It works by considering all possible moves that a player could make, and then calculating the minimum score that the opponent could achieve as a result of each move. The player then chooses the move that maximizes their score while minimizing the opponent's score.
One way to improve the efficiency of the minimax algorithm is through the use of alpha beta pruning. This technique involves maintaining two values, alpha and beta, which represent the minimum and maximum scores that the player can expect, respectively. If at any point during the search, it becomes clear that the current score is worse than the alpha or beta values, the search can be stopped, as the player will not choose a move that results in a worse score.
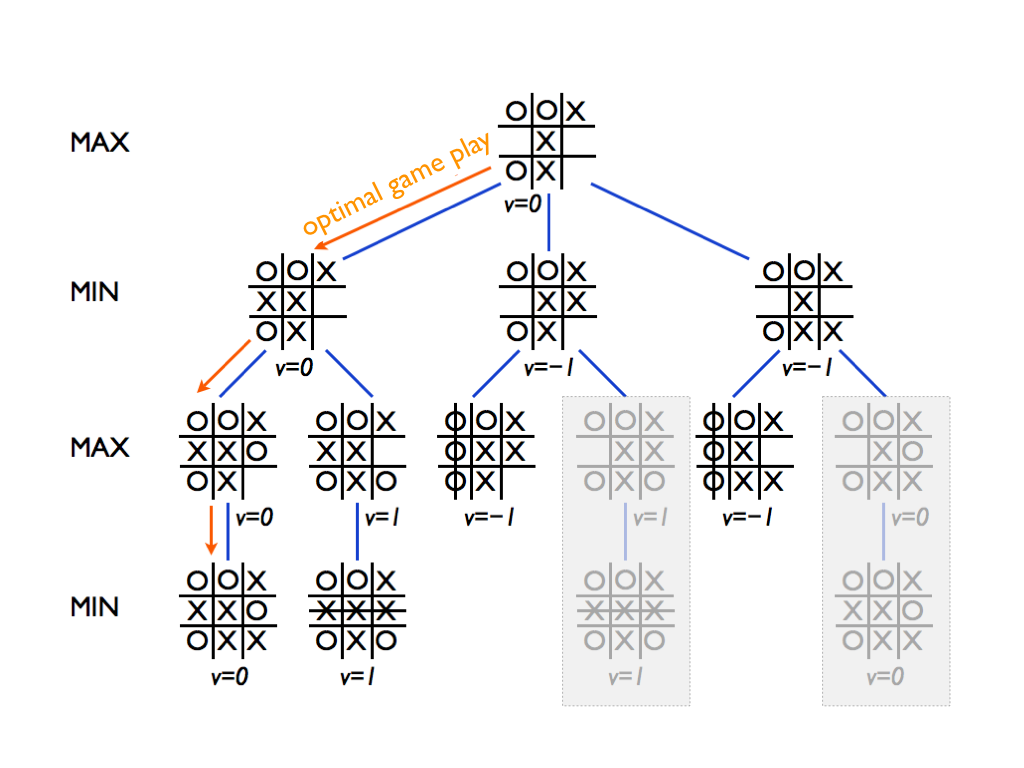
For example, consider a simple two-player game where the players take turns placing coins on a board, and the player who gets three in a row first wins. The minimax algorithm would search through all possible moves, calculating the minimum score that the opponent could achieve as a result of each move. Using alpha beta pruning, the search could be stopped as soon as it becomes clear that the current score is worse than either the alpha or beta values.
In this example, assume that it is the first player's turn, and that the alpha and beta values are initially set to negative infinity and positive infinity, respectively. The first player considers placing a coin in the top left corner of the board. This results in a score of -1 for the first player and 1 for the second player, as the second player now has a chance to block the first player's three in a row. The first player then considers placing a coin in the top center of the board, resulting in a score of 0 for both players.
At this point, the alpha value is updated to 0, as this is the minimum score that the first player can expect. The first player then considers placing a coin in the top right corner of the board, resulting in a score of 1 for the first player and -1 for the second player. The first player chooses this move, as it results in the highest score while minimizing the opponent's score.
Overall, the minimax algorithm is a powerful tool for decision-making and game theory, and the use of alpha beta pruning can significantly improve its efficiency by allowing the search to be stopped early when it becomes clear that a move will not result in the optimal outcome.