The Fibonacci sequence is a mathematical concept that has fascinated researchers for centuries. It is a series of numbers in which each number is the sum of the previous two, starting with 0 and 1. The Fibonacci sequence has a number of interesting properties and has been studied in a variety of fields, including mathematics, computer science, and biology.
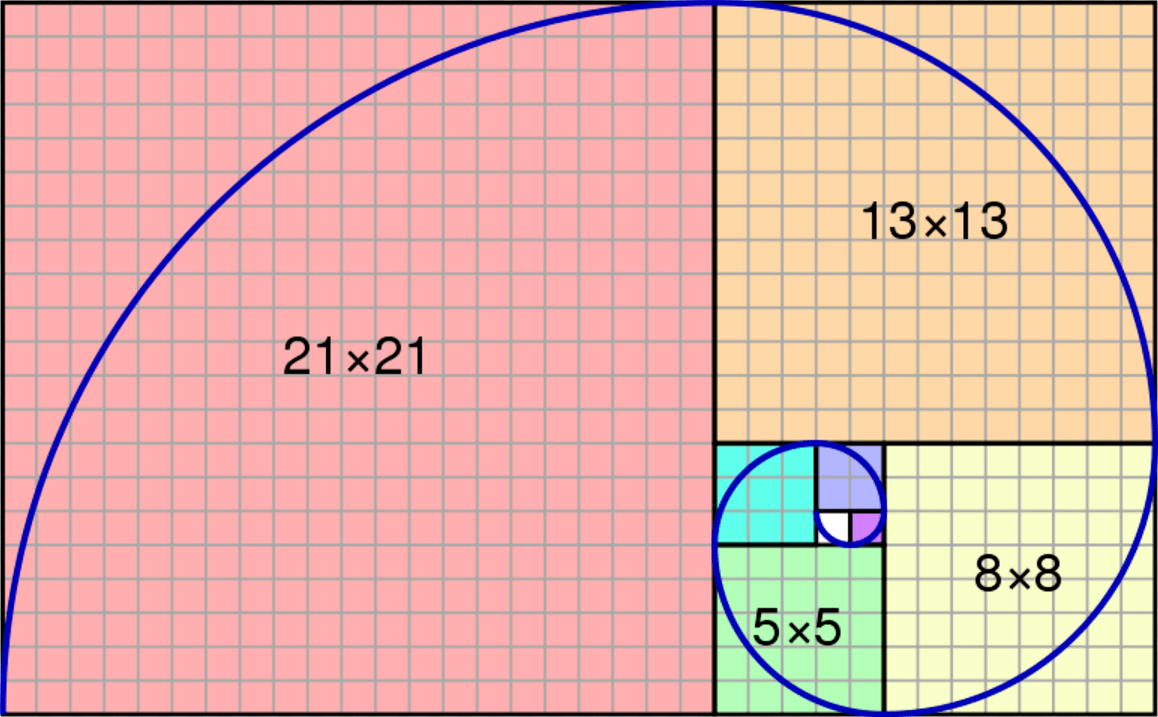
One of the most well-known properties of the Fibonacci sequence is its relationship to the golden ratio, which is a mathematical constant represented by the Greek letter phi (φ). The golden ratio is the ratio of the length of a line segment to the length of the longer segment into which it is divided, such that the ratio of the whole segment to the longer segment is the same as the ratio of the longer segment to the shorter segment. The golden ratio is approximately equal to 1.618, and it is thought to be aesthetically pleasing because it appears in many natural forms, such as the branching patterns of trees and the arrangement of seeds on a sunflower.
The Fibonacci sequence is closely related to the golden ratio because if you divide each number in the sequence by the one before it, the resulting ratio converges on the value of the golden ratio as the numbers become larger. This relationship has been used in a variety of applications, including the design of financial trading algorithms and the analysis of biological growth patterns.
Another interesting property of the Fibonacci sequence is its connection to the concept of recursion, which is a process in which a function is defined in terms of itself. The Fibonacci sequence can be defined recursively, meaning that each number in the sequence is determined by the previous two numbers. This property makes the Fibonacci sequence a useful model for understanding recursive algorithms, which are widely used in computer science.
In addition to its mathematical properties, the Fibonacci sequence has also been studied in the field of biology. Researchers have found that the Fibonacci sequence appears in the growth patterns of many natural forms, including the branching patterns of trees and the arrangement of seeds on a sunflower. This has led to the development of a branch of mathematics known as phyllotaxis, which studies the relationship between the Fibonacci sequence and the growth patterns of plants.
Overall, the Fibonacci sequence is a fascinating and deeply researched mathematical concept that has a wide range of applications in various fields. Its connection to the golden ratio and its use in the study of recursive algorithms make it an important tool for researchers in mathematics and computer science, while its presence in the growth patterns of plants has made it a subject of study in the field of biology.





:max_bytes(150000):strip_icc()/FIBONACCI-SEQUENCE-REVIEW-ILLUSTRATION-c655f399da6841979b1c83d253e09fd7.png)