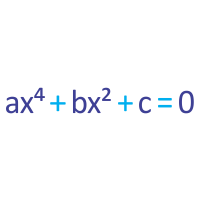An equation reducible to a quadratic equation is a type of mathematical equation that can be transformed into a quadratic equation through a series of algebraic manipulations. A quadratic equation is an equation in the form of ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable.
One way to determine if an equation is reducible to a quadratic equation is to attempt to rearrange the terms in the equation so that it is in the form of ax^2 + bx + c = 0. This can be done by using algebraic techniques such as factoring, completing the square, or using the quadratic formula.
For example, consider the equation 3x^2 + 6x - 9 = 0. This equation is already in the form of a quadratic equation and therefore is reducible to a quadratic equation.
On the other hand, consider the equation x^3 + 2x^2 + x - 1 = 0. This equation is not in the form of a quadratic equation, but it can be rearranged into the form of a quadratic equation through the use of factoring. Factoring the equation gives (x - 1)(x^2 + x + 1) = 0, which can be rewritten as x^2 + x + 1 = 0. This equation is now in the form of a quadratic equation and is therefore reducible to a quadratic equation.
Another example of an equation reducible to a quadratic equation is x^4 + x^2 - 1 = 0. This equation can be rearranged through the use of the quadratic formula to give (x^2 - 1)(x^2 + 1) = 0, which can be rewritten as x^2 + 1 = 0.
In summary, an equation reducible to a quadratic equation is a type of equation that can be transformed into the form of a quadratic equation through the use of algebraic techniques such as factoring or the quadratic formula. These types of equations are important in many areas of mathematics and have a wide range of applications in science, engineering, and other fields.