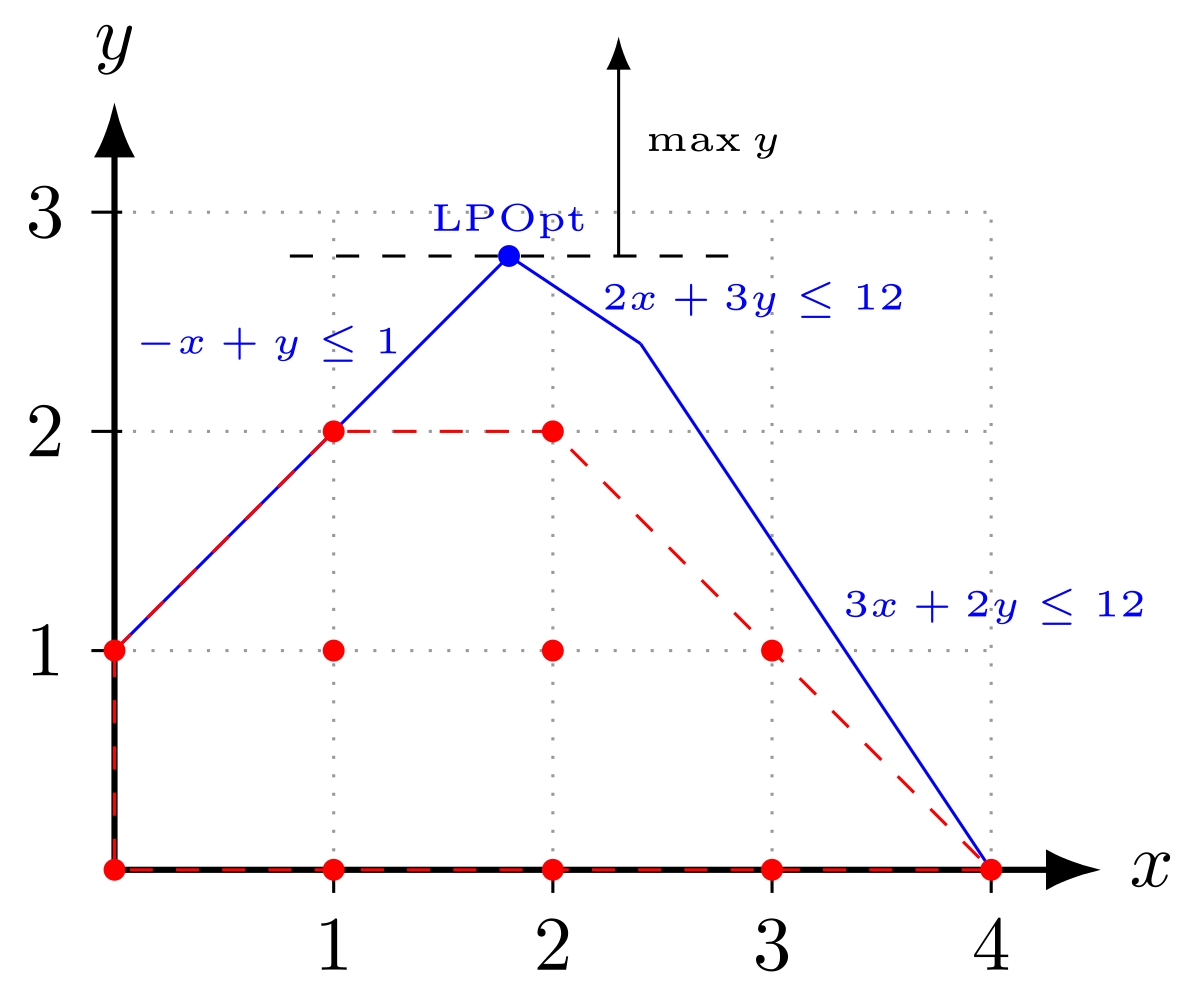
Linear programming is a mathematical optimization technique used to find the maximum or minimum value of an objective function, subject to a set of constraints. In linear programming, the objective function and the constraints are all linear, meaning they are made up of linear combinations of variables.
Maximization and minimization are two common goals in linear programming. Maximization refers to the process of finding the maximum value of the objective function, while minimization refers to the process of finding the minimum value.
One key difference between maximization and minimization in linear programming is the direction of the objective function. In maximization problems, the objective function is set up such that an increase in the variables leads to an increase in the objective function. In minimization problems, an increase in the variables leads to a decrease in the objective function. This means that, in a maximization problem, we are looking for a combination of variables that leads to the highest possible value of the objective function, while in a minimization problem, we are looking for a combination of variables that leads to the lowest possible value.
Another difference between maximization and minimization in linear programming is the way in which the constraints are set up. In a maximization problem, the constraints are set up such that they limit the variables from taking on values that would lead to a higher objective function value. In a minimization problem, the constraints are set up such that they limit the variables from taking on values that would lead to a lower objective function value.
Overall, maximization and minimization in linear programming involve finding the maximum or minimum value of the objective function, subject to a set of constraints. The direction of the objective function and the way in which the constraints are set up are key differences between the two goals. Linear programming is a powerful tool that is used in a variety of fields, including economics, operations research, and engineering, to solve complex optimization problems.